Manin's principle in the functional case
Notation: let ![]() be a prime number,
be a prime number, ![]() ,
,
![]() a smooth
projective curve over
a smooth
projective curve over
![]() ,
,
![]() .
A point
.
A point
![]() induces a function
induces a function
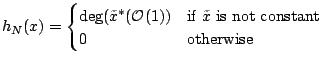 |
Now let ![]() be a smooth, geometrically integral projective variety over
be a smooth, geometrically integral projective variety over
![]() , let
, let
![]() be an open subset, and define
be an open subset, and define
Results
Answers are positive if
Simplest example:
![]() . Let
. Let ![]() be the genus of
be the genus of
![]() .
.
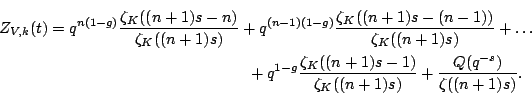
Work in progress with A Chambert-Loir.
The ring of motivic integration
(Kontsevich, Denef, Loeser)
Definition:
Let ![]() be a field, and let
be a field, and let
![]() be the ring with generators
be the ring with generators ![]() as
as ![]() ranges
through varieties
over
ranges
through varieties
over ![]() , subject to the relations
, subject to the relations
![]() if
if ![]() and
and
![]() , for
, for ![]() open in
open in ![]() , and with multiplication given by the
product of varieties.
, and with multiplication given by the
product of varieties.
(Note: De Jong pointed out some problem with this definition in positive characteristic.)
Now let
![]() ,
,
![]() . Define a filtration by
. Define a filtration by
Motivic height
Let the notation be as in Section ![]() .
Given an embedding
.
Given an embedding
![]() we get a
height
we get a
height
![]() . Given an open
. Given an open
![]() ,
we can define varieties
,
we can define varieties ![]() such that for all
such that for all ![]() ,
,
![$\displaystyle Z_{U, k}(T) = \sum_{n \in \mathbb{N}} [U_n] T^n \in \mathcal{M}_k[[T]].$](img60.gif) |
![$\displaystyle Z_K(T) = \sum_{i \in \mathbb{N}}[\mathcal{C}^{(i)}] T^i$](img65.gif) |
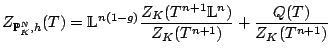 |
![\begin{proposition}[Kapanov]
\begin{enumerate}
\item $Z_K(T)$\ is a rational f...
...thbb{L}T) = \mathbb{L}^{1-g} T^{2-2g} Z_K(T)$.
\end{enumerate}\end{proposition}](img69.gif)
![\begin{theorem}[Follows from Kapanov]
Let $G$\ be a split semi-simple proper al...
...ption of its value similar to the functional case.
\end{enumerate}\end{theorem}](img70.gif)
![]()
Hope: generalize this to smooth cellular varieties over ![]() .
.
Remark: Batyrev has a nice idea to attack this when ![]() is defined
over
is defined
over ![]() . But we have no idea what the relevant harmonic analysis is in
this case.
. But we have no idea what the relevant harmonic analysis is in
this case.
A realization map
Suppose
![]() , and define a map
, and define a map
![]() ,
,
![]() . Then we get a map
. Then we get a map
Back to the
main index
for Rational and integral points on higher dimensional varieties.