The recipients of the 2025 Alexanderson Award are Raphaël Beuzart-Plessis, Yifeng Liu, Yichao Tian, Liang Xiao, Wei Zhang, and Xinwen Zhu. These members of the AIM SQuaRE “Geometry of Shimura varieties and arithmetic application to $L$-functions” are recognized for two papers:
“Isolation of the cuspidal spectrum, with applications to the Gan-Gross-Prasad conjecture” by Beuzart-Plessis, Liu, Zhang, and Zhu, published in the Annals in 2021; and
“On the Beilinson-Bloch-Kato conjecture for Rankin-Selberg motives” by Liu, Tian, Xiao, Zhang, and Zhu, published in Inventiones in 2022.
Mathematics is about relationships. Applied mathematics seeks relationships between the real world and mathematical objects, and from those mathematical objects, to provide useful information about the real world. Much of pure mathematics is about relationships between different mathematics objects. When the relationship is surprising, such mathematics is considered “deep.”
A classic example is the Birch and Swinnerton-Dyer (BS-D) conjecture, which concerns elliptic curves: think equations of the form $E:\ \ y^2 = x^3 + a x + b$, where $a$ and $b$ are rational numbers and the cubic has no repeated roots. Natural questions are: Does that equation have a solution where $x$ and $y$ are also rational numbers? If so, is the number of solutions finite or infinite? And if there are infinitely many, what is the rank (a property similar to dimension) of the set of solutions?
The BS-D conjecture asserts that the answers to those questions are hidden in the analytic properties of a function $L(s,E)$ which can be derived from the elliptic curve. That function can be graphed, just like the polynomials and trigonometric functions students learn to graph in high school. By “analytic properties” of the function we mean answers to questions like: Where is it positive or negative? Where is the graph curving up or curving down? Where does the graph cross the axes? The BS-D conjecture uses those properties to deduce information about the rational solutions to the equation $E$. By any reasonable measure, that is a surprising connection.
The story is even richer: there are other types of objects which have $L$-functions, two of which are called modular forms and Galois representations. We can represent these relationships with a diagram:
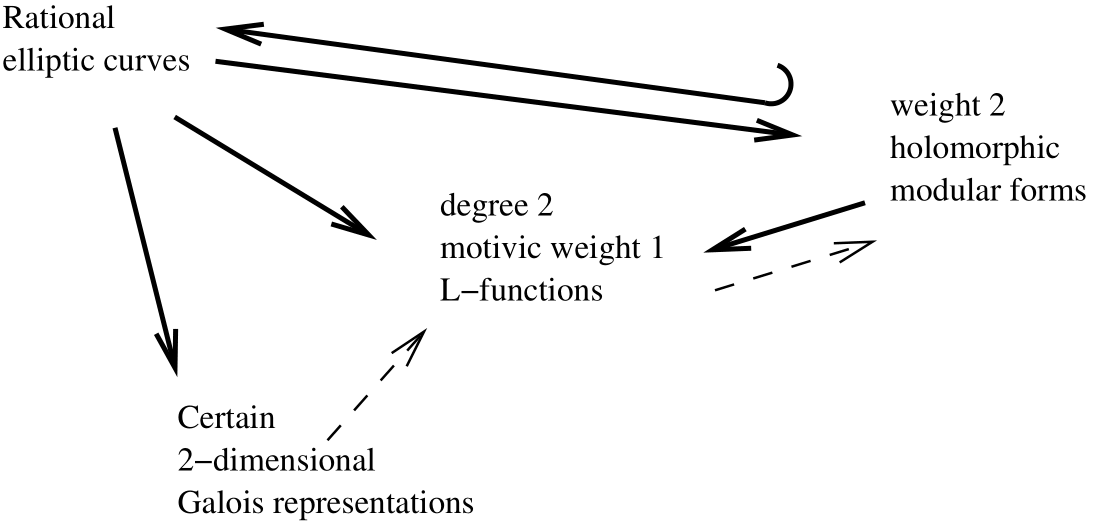
Some special cases of the Langlands program. Solid arrow: there exists a construction which directly produces the target object. Hook arrow: the construction only works for some of those objects. Dotted arrow: the target object may not be known to have all the necessary properties.
The collection of relationships between the types of objects in the diagram is known as the Langlands program, initially formulated by Robert Langlands in the late 1960s. The cases shown above are largely proven, but those are the simplest instances of a wide-ranging web of conjectured connections. Very few other cases have been proven.
Historically the BS-D conjecture came first, but a more useful way to view it is that the Langlands program provides a framework of connections between objects. The BS-D conjecture describes how properties of one of those objects gives information about a related object.
The winning team for this year’s Alexanderson Award made significant progress on two generalizations of the BS-D conjecture, known as the Beilinson-Bloch-Kato (BBK) conjecture and the Gan-Gross-Prasad (GGP) conjecture. To see how these conjectures relate to the BS-D conjecture, we consider a more abstract version of the connections conjectured by the Langlands program in Figure~2.
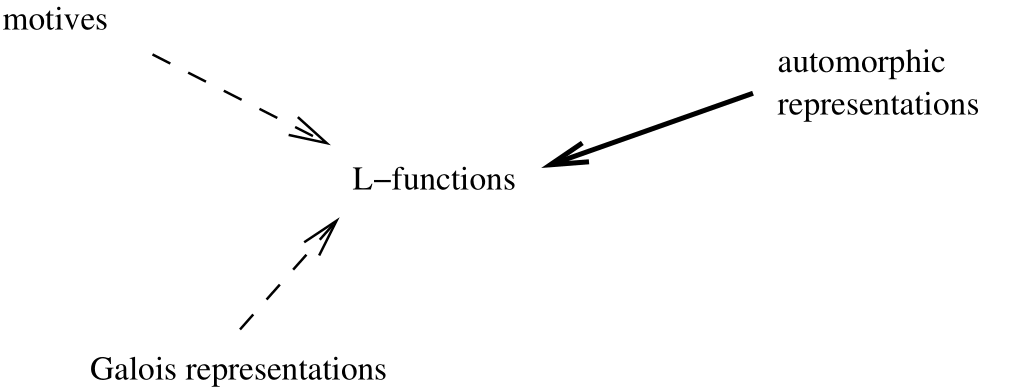
The general case of the Langlands program.
In this perspective, $L$-functions are the “glue” that provides an intermediate step in connecting the other objects: those objects are related if they have the same $L$-function. Unlike the special case shown above, no constructions have been found which provide direct connections between the objects: the relationships are indirect, via having an association to the same $L$-function.
For the BBK conjecture, one begins not with one equation, but with a system of equations — more precisely an algebraic variety. That is a type of “motive,” as in the diagram. That algebraic variety has an $L$-function, and the BBK conjecture relates analytic properties of that $L$-function to information about solutions to that system of equations, in a manner very similar to the BS-D conjecture.
For the GGP conjecture, the starting point is an automorphic representation, which is a generalization of a modular form. That object has an $L$-function, as indicated in the diagram. The GGP conjecture uses information about the $L$-function to deduce information about the automorphic representation. The connection to the BS-D conjecture is more subtle.
Both the BBK and the GGP conjectures are quite general and apply to a wide range of varieties and representations, respectively. The results of the Alexanderson Award winners do not resolve the general case, but do cover several situations, the details of which are too intricate to present here. However, their results have special cases which are easier to describe. Consider the case of two elliptic curves, $E_1$ and $E_2$, and instead of insisting on having rational coefficients in their equations, allow those coefficients to be algebraic numbers. Together those elliptic curves have an $L$-function denoted $L(s, E_1 \times E_2)$. The analytic condition in their theorem is quite simple: Is $L(\frac12, E_1 \times E_2) = 0$? If the answer is no, then one of their results states that yet another object, known as the Bloch-Kato Selmer group, is 0. That proves a case of the BBK conjecture.
Another result considers two automorphic representations $\Pi_1$ and $\Pi_2$, which together have an $L$-function $L(s, \Pi_1 \times \Pi_2)$. They show that when $L(\frac12, \Pi_1 \times \Pi_2) \ne 0$, then a particular aspect of the GGP conjecture is true: the stable case of the conjecture for the product of unitary groups $U(n)\times U(n+1)$.


